1. Longitud de la cadena (número de eslabones): L
Transmisión de bobinado

Al utilizar una transmisión de bobinado de dos ejes

• (1) Cuando la distancia entre centros y el número de dientes de ambos piñones están fijos

  L = Z + Z' 2 + 2C + Z - Z' 6.28 ² C
  

• (2) Cuando el número de eslabones y dientes de la cadena es fijo
  C = 1 8   2L - Z - Z' + (2L - Z - Z')² - 8 9.86 (Z - Z')²
  Cualquier parte fraccionaria (parte decimal) del valor L calculado se redondeará y se contará como un enlace, incluso si es pequeña.
  Si hay un número impar de eslabones, se debe utilizar Eslabón acodado, pero si es posible, cambie el número de dientes de la rueda dentada o la distancia entre centros para que sea un número par de eslabones.

Transmisión por engranaje de pasador

Al utilizar una cadena con un accesorio enrollado alrededor del exterior del tambor

L = 180° tan^-1 P D + 2S

• P: Paso de cadena
• D: Diámetro exterior del tambor
• S: Altura del accesorio

• * Redondea L al número par de eslabones.
• * Al instalar el accesorio de cadena en el exterior del tambor, inserte las cuñas de manera uniforme para ajustar el encaje.

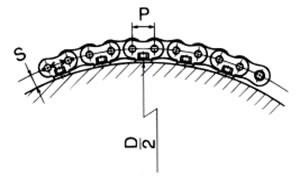
2. Velocidad de la cadena: V

V = P × Z' × n 1000 (m/min)

3. Tensión de la cadena a la potencia nominal del motor (kW) y a la velocidad de rotación nominal: Fm

Fm = 60 × kW V (kN)

Fm = 6120 × kW V (kgf)

4. Momento de inercia de la carga I(GD) ²)de
Convertido en eje del motor principal
Momento de inercia: I _ℓ (GD ²_ℓ)

I_ℓ = M × V 2πn₁ ² (kg・m²)

GD²_ℓ = W × V πn₁ ² (kgf・m²)

5. Par nominal del motor principal: Tn

Tn = 9.55 × kW n₁ (kN・m)

Tn = 974 × kW n₁ (kgf・m)

6. Par de trabajo: Tm

Tm = Ts(%) + T _max (%) 2 × 100 × Tn (kN・m)
o
Tm = Ts(kN·m) + T _max (kN·m) 2 (kN·m)

Tm = Ts(%) + T _max (%) 2 × 100 × Tn (kgf・m)
o
Tm = Ts(kgf·m) + T _max (kgf·m) 2 (kgf·m)

7. Tensión de la cadena debido al par de arranque: Fms

Fms = Ts(%) × i {d/(2 × 1000)} × 100 × Tn × 1(kN)
o
Fms = Ts(kN·m) × i d/(2 × 1000) × 1(kN)

Fms = Ts(%) × i {d/(2 × 1000)} × 100 × Tn × 1(kgf)
o
Fms = Ts(kgf·m) × i d/(2 × 1000) × 1(kgf)

Tensión de la cadena debido al par de frenado: Fms

Fmb = T _b (%) × i {d/(2 × 1000)} × 100 × Tn × 1.2*(kN)
o
Fmb = T _b (kN·m) × i d/(2 × 1000) × 1,2*(kN)

* es una constante

Fmb = T _b (%) × i {d/(2 × 1000)} × 100 × Tn × 1.2*(kgf)
o
Fmb = T _b (kgf·m) × i d/(2 × 1000) × 1,2*(kgf)

* es una constante

8. Tiempo de aceleración: ts
Si se conoce el tiempo de aceleración, utilice ese tiempo.

ts = (Im + I_ℓ) × n₁ 9550 × (Tm - T_ℓ) (s)

ts = (GD²m + GD²_ℓ) × n₁ 375 × (Tm - T_ℓ) (s)

9. Tiempo de desaceleración: t _b
Si se conoce el tiempo de desaceleración, utilice ese tiempo.

±: Para cargas negativas como cargas colgantes
Digamos -T _ℓ.

t_b = (Im + I_ℓ) × n₁ 9550 × (Tb ± T_ℓ) (s)

t_b = (GD²m + GD²_ℓ) × n₁ 375 × (Tb ± T_ℓ) (s)

10. Aceleración

• Movimiento lineal: αs
• Movimiento de rotación: ωs

Se asume una aceleración en línea recta.

De lo contrario, calcule con la aceleración máxima.

Movimiento lineal (aceleración de la carga) αs = V _ℓ ts × 60

Movimiento de rotación (velocidad angular del eje del motor primario) ω = 2 π × n1

Movimiento de rotación (aceleración angular del eje del motor primario) ωs = ωts × 60

11. Desaceleración

• Movimiento lineal: αb
• Movimiento de rotación: ωb

Se asume una aceleración en línea recta.

De lo contrario, calcule en la desaceleración máxima.

Movimiento lineal (desaceleración de la carga) αb = V _ℓ tb × 60

Movimiento de rotación (velocidad angular del eje del motor primario) ω = 2 π × n1

Movimiento de rotación (desaceleración angular del eje del motor primario) ωb = ωtb × 60

12. Tensión de la cadena durante la aceleración: Fs

Movimiento lineal Fs = M × αs 1000 + Fw

Movimiento de rotación Fs = I _ℓ × ωs × i 1000 × d 2 × 1000 + Fw

Movimiento lineal Fs = M × αs G + Fw

Movimiento de rotación Fs = GD ²_ℓ /4 × ωs × i d 2 × 1000 × G + Fw

Tensión de la cadena durante la desaceleración: Fb

Movimiento lineal Fb = M × αb 1000 + Fw

Movimiento de rotación Fb = I _ℓ × ωb × i 1000 × d 2 × 1000 + Fw

Movimiento lineal Fb = M × αb G + Fw

Movimiento de rotación Fb = GD ²_ℓ /4 × ωb × i d 2 × 1000 × G + Fw

13. Corrección kW (para selección general)

14. Tensión de la cadena de compensación

Tensión de la cadena de corrección del motor primario: F'm

Tensión de la cadena corregida a partir del par de arranque: F ms

Tensión de la cadena de corrección por par de bloqueo: F'mb

Tensión de la cadena de compensación del accionamiento del carro: F'c

Tensión de la cadena corregida durante la aceleración: F

Tensión de la cadena corregida durante la desaceleración: F'b

Tensión de cadena corregida por carga: F'w

F'w = M × Ks × Kn × Kz × G 1000 (kN)

F′w = W (o Fw) × Ks × Kn × Kz (kgf)

Si se desconoce la masa M {peso W}, calcule el par de torsión del eje T = Tn × i (kN・m) {kgf・m} a partir del par de torsión nominal Tn del motor primario.
En lugar de W, utilice F = 2T/d.

15. Relación de inercia: R

R = I_ℓ Im

R = GD²_ℓ GD²m

16. Conversión del momento de inercia (I) y efecto volante (GD ²)